2019年度 千葉県高校入試 問題の分析

国語 岡部 順介
前期 スピードと正確さを兼ね備えた読解法を身につける

大問2・3 漢字の読み書きの問題
漢検の学習が有効。語彙を増やすことは、文章読解のスピードと、内容把握の精度の向上にもつながる。
大問4 国語の知識に関する問題
文法、敬語、漢文の訓読、漢字の基本的な知識が問われた。敬語は尊敬語に直す際、「一文節」という条件に気をつける。
大問5 論説文の読解
詩を深く味わうための方法について、筆者の考えをとらえる。話題と結論を押さえる練習ができていれば、比較的読み取りやすい内容。(1)は、空欄補充問題。空欄Aの「詠む」、空欄Bの「誦む」の詳しい説明は、空欄がある段落の次の段落以降にある。(2)も空欄補充問題。空欄Cの前後と似た内容が前の段落にある。(3)は、傍線Dを含む文と、その次の文を比較することで、筆者の考えが明らかになる。(4)は、設問の空欄あとの「詠む人を感動させる」を手がかりに、本文から似た内容を探して答える。(5)は、35字以内で答える記述問題。傍線Fの前の指示語の内容を確認し、設問で示された形式通りに答えること。(6)は、本文の内容と一致するものを選ぶ問題。話題と結論が押さえられていれば、素早く解答できる。
大問6 小説の読解
登場人物が多いので、前書きの部分で関係性を整理したうえで本文を読み進める。各人物の会話や動作から人物像と心情をとらえる。(1)は、傍線Aの前の「ふだんはあまり顔にも言葉でも感謝を示さない」久兵衛の様子から答える。(2)は、傍線Bのあとの久兵衛の会話をもとに答える。(3)は、傍線Cの前の「菓銘はふつう作り手がつけるものだ」という久兵衛の会話や、傍線Cのあとの「菓銘にそんな重々しい意味があったとは知らなかった」から考える。(4)は、空欄Dのあとの「少し照れくさい」「菓子の形状に棗(なつめ)の花と実を使った久兵衛の思いも名前に入れたい」に注目。(5)Ⅰは、設問の空欄前の「思ったことをすぐ口に出してしまう」を手がかりに答える。Ⅱは、設問の空欄前に「餡の味わい」とあるので、本文中の菓子を食べている場面から安吉に関する描写を探す。(6)は、10字以上、20字以内で答える記述問題。「おまさ」が期待している内容を書く。傍線Eの前の「おまさ」の会話をまとめればよい。
大問7 古文の読解
注や設問を参考に、主語を確認しながら本文のおおまかな内容をおさえる。また事前に基本的な助詞や助動詞の意味を押さえておくことで、本文理解の助けにしたい。
大問8 作文
「巨人の肩の上に立つ」というたとえは、私たちが「先人の残した文明の遺産を譲り受けた立場にある」ことを言い表している。それを「これからの生活にどう生かしたいか」について、自分の考えを書く。条件を正確に読み取り、求められていることを正しく理解して記述する力が求められている。
全体を通して
例年通りの傾向が続いている。正しい読解法を身につけ、スピードと正確さに磨きをかけることで高得点を目指したい。聞き取り問題・国語の知識・論説文の読解・小説の読解・古文・作文と、バランスよく学習していく必要がある。
社会 岡部 順介
前期 教科書・資料集の読み込みが高得点への絶対条件
大問1 三分野総合
例年通り、千葉県について取り上げ、地理・歴史・公民を融合させた問題だった。「資料の読み取り問題」も昨年同様に出題された。ただし、資料の読み取りの基本である「全国と比較すると多い・少ない」や「割合が高い・低い」に目をつければ解きやすい問題であったと思われる。
大問2 日本地理
県庁所在地を問うもの、山口県の地形図を読み解くもの、静岡県、愛知県、岐阜県、三重県で生産されているものを選ぶ問題が出題された。土地の起伏を断面図に表した問題では、次の2点をおさえる。まず、Y地点の高さが260メートル近くであること、次にXY地点の間に100メートル以下になる箇所がいくつあるかを確認すればよい。
大問3 世界地理
ダイヤモンドの生産の割合のグラフを見て国を選ぶもの、中国の北部・南部・西部での農業の様子を選択するものなど、各国の産業の特徴をつかんでいないと解けない問題があった。教科書だけでなく資料集にまでしっかり目を通しておく必要がある。
大問4 歴史(古代~近世)
縄文時代から江戸時代までのパネルを見て答える問題。基本的な問題だけでなく、勘合貿易に関する記述問題や江戸時代の年代の並べ替え、そして特筆すべきは平成から元号が変わるということで、日本の最初の元号(大化)と同じ世紀に起こった世界の出来事を問う問題が出題された。教科書の太字の用語だけでなく、もう一歩踏み込んだ知識を身につける必要があるだろう。
大問5 歴史(近代~現代)
幕末~戦後までが取り上げられた。昨年同様、大問5は全般的に難問が多かった。特に(5)のマルタ会談はヤルタ会談と混同しやすく、教科書の索引にも出てこない用語。教科書の隅々まで読み込んでいないと自信を持って答えることはできなかっただろう。
大問6 公民(経済)
(1)は需要と供給の問題、(2)は為替相場の計算問題、(3)は資料の読み取り問題が出題された。(1)(2)は基本的な問題なので、あせらずに解けば大丈夫だろう。(3)は年金給付に関するアンケート結果を読み取る問題。①②③の回答文が長いので、一度整理してから読む必要がある。社会保障は少子高齢化とも関係するので、年金支給に必要な財源の確保が必要なことも理解しておこう。
大問7 公民(政治)
日本国憲法や人権思想、裁判員制度について問われた。基本的な問題であり、確実に点を取りたい内容が並ぶ良問であった。
大問8 公民(国際社会)
(1)はBRICSを答えさせる問題、(2)は南南問題を選択させる問題が出題された。(1)は国名が問題文に書かれているので、その頭文字をアルファベットで並べていけば解答できる。(2)は「発展途上国どうしでの経済格差」とあるので、南北問題との区別はつけられただろう。
全体を通して
本年度の問題数及び形式は例年と同様で、特に大きく変わった点は見られなかった。どの分野も教科書で基本的な知識を身につける必要があるのは言うまでもないが、資料問題や地形図の読み取り・文章記述問題など、実際に作業をして準備しておくべき問題をいかに落とさないか、スムーズに解けるかが点数の差につながる。そのためには日頃から教科書とともに資料集にも目を通したうえで問題にあたり、インプットした知識をアウトプットする経験を積み重ねていく必要がある。
英語 村上 献
前期 リーディング・ライティング・リスニングをバランスよく学習

大問1~4 リスニング問題
全体の約3分の1の配点。大問1は対話を聞き、その状況に応じた受け答えを選ぶ問題で、内容は基本的。大問2は絵やグラフの内容に関する対話から適した内容を答える問題で、大問3は対話から状況と内容を読み取る問題。大問4は英文を聞いて、英単語を記述させる問題。出題された単語は、highest, river, October, healthであった。
大問5 文法知識を問う問題
(1)、(2)は英単語を正しい形にする語形変化問題。(3)、(4)、(5)は英単語を正しい語順に並べかえる整序問題。(1)は前置詞の後ろの動詞を動名詞に変えさせる問題で、“practice”を“practicing”にする。(2)は“music”を音楽家の“musician”に変える問題。正しくつづれるように普段から基本単語を練習しておきたい。(3)は原級を使った表現、(4)は疑問詞を用いた疑問文、(5)は不定詞など、広く文法の知識を問われた。
大問6 対話形式の英作文問題
今年のテーマは、留学生のジェイの「一緒に数学を勉強したいか」という質問に、日本人学生ダイチの立場で英文を書く問題。ダイチが提案に対して少し困惑している様子や、次の日のテストの予定、英語の教科書を持っていることに注目しながら書くとよい。文の数に制限はないが語数には制限がある(20語程度)ので、ある程度まとまりのある長い文を書く必要がある。配点が8点と高く、また部分点もあり得点差がつきやすいので、色々なテーマで練習しておく必要がある。
大問7 短い3種類の文章読解問題
it is … to ~や関係代名詞など文法を総合的に理解しておく必要がある。出題形式は例年通り。(1)の適語選択問題は空所の前後をしっかり読むことが重要。(2)①は英語の質問に英語で答える問題で、thinkをwant toに置きかえて考えられたかがポイント。(3)はお店から送られてきた割引カードに関する内容一致問題で、割引が適用される条件をしっかりと読み取る必要があった。
大問8 長文問題
留学生のフィオナが「学校で食べるお弁当」について書いた日記を読んで答える。問題形式は、適語補充と内容一致。(1)はenjoyの後ろは~ing形になること、空欄直後のatに着目できたかがポイント。(3)の内容一致問題は、四角枠内の手順だけでなくその後ろの英文もしっかりと読む必要があった。
大問9 対話形式の読解問題
空所に合う英文を選ぶ問題。マサルとマサルの家にホームステイしているアメリカ人のジョーが、“soccer”と“football”の国による意味の違いについて話している。空所の前後のつながりを考えることがポイントで、また代名詞が何を示しているかを把握することが求められた。
全体を通して
中学校で習う内容がバランスよく出題されている。リスニング問題の内容自体は平易だが、読まれる速度がかなり速い。英作文は自由度が高く、ポイントを絞って書くことが難しい。どちらも直前の勉強だけでカバーすることは厳しく、早い段階での練習が不可欠である。併せて中学1年生からの文法事項も整理しておくこと。
数学 池田 慶
前期 中1・2の学習内容で7割解ける! 説明・証明が自分の言葉で書けることが合否の差になる!

大問1 計算問題 6問
基本的な計算問題。際立った問題はない。2次方程式の解の公式をしっかり使えるようにする。
大問2 資料の分析・反比例の変化の割合・連立方程式の利用・確率・作図
いずれの設問も中1~2で学習する内容であった。これまでの学習準備で、解くための工程を迷いなくできるかが重要。資料の分析は4択になっており複雑な計算も必要としない簡単な内容だった。
昨年同様、確率はさいころ2個の問題。作図は例年程度の難度、昨年よりは難しくなった。どのような直線を引けばよいかのイメージをしっかりもって、直線を引くためのもう1つの点をどう取るかがポイントだが、色々なアプローチが可能なので、解答例は多岐にわたると思われる。
作図を除いた4問は、いずれも過去に類似問題が多くある。かかる時間と正答率は他県、他校の入試問題に多く触れることで十分対応可能。
大問3 関数
放物線と直線による一般的な問題。式、座標をスムーズに出せるかが肝心。等積変形の内容が含まれており、学校でも学習はするが、教科書レベルでは対応が難しかった。とはいえ、関数に慣れている生徒にとってみれば今年の内容は、昨年の比を利用する問題よりも取り組みやすい設問だったといえる。
大問4 平面図形 ひし形と平行四辺形・証明
近年、円が出題されていたが、今年は平行四辺形であった。「平行」が解くためのキーになっており、錯角や同位角などを使った証明の記述を練習しておかないと、『証明の続き』がうまく書けない。千葉県は単純な1つ2つの工程で書ける証明問題を出さないので、合同や相似だけでなく、平行、図形の成立の証明などもしっかり練習しておくことが有効。
(2)は相似を利用して長さを求める難問、時間効率を考えると捨てる勇気も必要。
大問5 空間図形
例年、高い確率で「規則性」の問題が出題されていたが、今年は大きく路線を変えてきた。空間図形における体積の基本公式さえ使えれば(1)(2)は難しくはなかったが、逆を言うと公式が使えないと1問も出来ない内容だった。また(2)の「理由を式とことばで書きなさい」は千葉ではこれまで穴埋め形式だったが、今年はすべて記述での出題形式で、どう書けばよいのか?で悩んだ受験生も多かったと思われる。また(3)は中学受験などではよく出題される、水がこぼれる量についての問題だが、【おもりの円柱の高さ】と【あふれた水の量】を求める方法で悩むポイントがあり、それぞれは断面の図をイメージすることで、中1までの学習内容で解くことができた。
大問5(3)
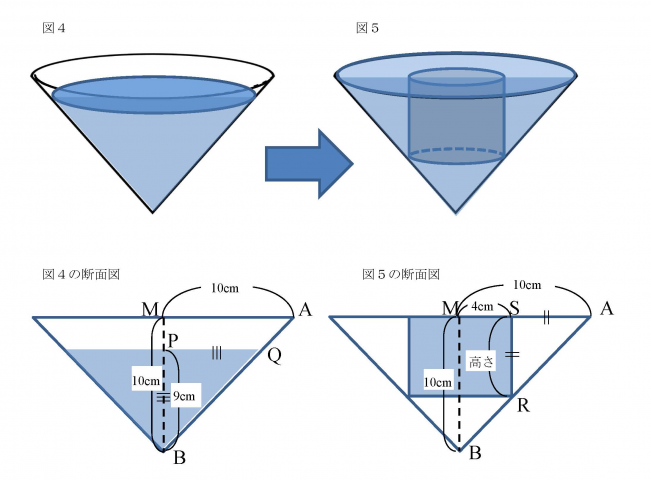
図4は底面の半径10cm,高さ10cmの円錐の容器に水面の高さが9cmになるまで水をいれたものである。その中に底面の半径4cmの円柱の形をしたおもりを,底面を水平にして静かに沈めると,容器から水があふれ出たあと,図5のように円柱の形をしたおもりの底面と水面の高さが等しくなった。
このとき,容器からあふれ出た水の体積を求めなさい。
考え方
「もともと入っていた水におもりの円柱分の水を加えると、容器に収まらずに水があふれた」と考えるとイメージしやすい。
入っていた水の体積 <図4の断面図より>
△QBPは直角二等辺三角形よりPB=PQ=9 求める体積は円錐なので9×9×9×π×1/3=243π
おもりの体積 <図5の断面図より>
△SARは直角二等辺三角形よりSA=SR=6 求める体積は円柱なので4×4×π×6=96π
容器の体積
求める体積は円錐なので10×10×10×π×1/3=1000/3π
あふれた水の体積
【入っていた水の体積】+【おもりの体積】-【容器の体積】=【あふれた水の体積】
<式>243π+96π-1000/3π=1017/3π-1000/3π=17/3π 答え. 17/3π cm3
全体を通して
大問1・2・3まではそこまで難しい問題も少ない。悩む時間を最小限にして大問4の証明や大問5の立体図形に時間を割きたい。過去問をしっかりこなし、出題傾向・時間配分・公式の確認などを事前に行うことが重要。
志望校の難易度にかかわらず、基本的な問題を落とさないことを目標にする。
理科 池田 慶
今年の前期は、例年出題される傾向にあった「規則性」が出題されなかった。
規則性の問題は長文からなる「ルール」が理解しにくい内容が多く、読解までに時間がかかる問題が多かったのに対し、今年の空間図形は文面の理解はしやすいが図の状況を理解しづらいのと、分数や大きな数の処理が手間取る問題であった。
立体の断面について自分でイメージを書くことで中1までの学習内容で必要な情報を得ることが可能だが、そもそも断面図について学校の授業でふれる機会がない。つまり、他の入試問題などにふれ、普段から立体の図形を面で切る訓練が必要になる。
全体を通して中1・2で学習する内容で処理できる問題が多くあり、大問4を除いた設問は公式をはじめとする基本的考え方ができれば、かなり点を取れる内容だった。
反面、大きな数や分数の処理をミスなくできるスキルと、考え方を定型文ではなく、自分の言葉で書いて説明するスキルが高得点につながる問題構成だったといえる。
前期 勝負の分かれ目は教科書の読み込みと比例式の活用
大問1 小問集合
(3)はガスバーナーの正しい使い方に関する問題。毎年実験器具の使い方に関する問題が出題されるので、教科書に記載されている実験のページを良く読み、使い方を確認しておくとよい。
大問2 雲の発生
雲を発生させる実験からの出題。教科書に記載されている実験と非常に似ている問題だった。大問1と同様、実験のページを読んで理解をしておくことが重要。また、(4)の問題は「下線部bのしくみ」にある「気圧が下がる」という条件に合わないものを探すことで答えを導き出せるようになっていた。
大問3 回路とオームの法則
(1)はオームの法則、(2)は直列回路と並列回路それぞれにおける電流・電圧・抵抗の関係を正しく理解しているかがカギになる。(3)は測定結果の数値から回路のつくりを答える問題。電流が流れない端子間は抵抗器を接続していない。そのため、PR間・PS間・RS間から2つ選ぶことになるが、表の電流の値からPR間・PS間・RS間の抵抗はそれぞれ30Ω・20Ω・10Ωとなる。このことからPR間は、PS間とRS間の和になっているため、PS間とRS間を直列回路でつないだと読み取れる。
大問4 イオンと中和
中3で学習するイオンの単元からの出題だが、(1)は中1の学習内容からの出題だった。イオンの単元を学習する際には中1の気体の性質・中2の化学式を予め復習しておくと、理解が深まり(1)のような問題にも対応できるだろう。計算もなく、解答しやすい問題であった。
大問5 光合成と呼吸
光があたる所とあたらない所での酸素と二酸化炭素の増減を比べると、光合成と呼吸の量が推測できる。なお、(4)は対照実験である。袋の中の気体の割合が変化するのは鉢植えの植物が光合成・呼吸をしているためであり、袋から気体が漏れていないことを示すという目的に気づくことが出来れば、解答できる問題だった。
大問6 ばねにはたらく力と浮力
(1)(b)では、おもりAは何個であってもばねののびは整数となるが、おもりBは2個使ったときのみばねののびが整数で、さらに5cm以下になることをグラフから読み取れるかがポイントとなった。また、(2)(b)では、ばねばかりの値は物体にはたらく「重力と浮力の差」で求められるという知識が必要である。ただし、「合力の大きさ」という指定語句で、何と何の合力かを考えると正解にたどり着ける。
大問7 化学変化と質量
(1)は質量保存の法則が成り立つ理由を問われた。 (2)は正解率の低い問題になると思われる。①と②で共通するポイントは「比例」であった。
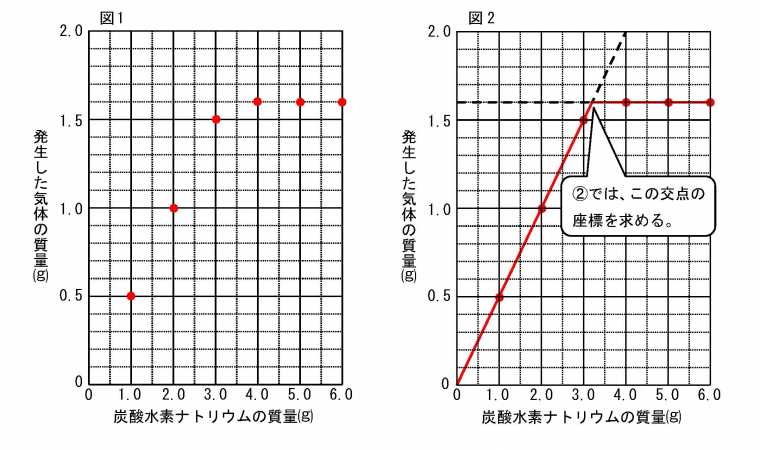
①では、まず下の図1のように問題用紙の表をもとにして点を打つ。そして下の図2のように、炭酸水素ナトリウムの質量と発生した質量が比例の関係になるグラフと、うすい塩酸が全て反応に使われたあとは発生した気体の質量が一定になるグラフを書く。どちらも直線であることが重要。
②では、反応に使われた炭酸水素ナトリウムが何gになるかを求めるとよい。これは図2における2つのグラフの交点を求めることにより導き出せる。交点は比例のグラフ上にあるので、比例式が使える。発生した気体が1.6gのときの炭酸水素ナトリウムの質量をxgとすると、グラフより発生した気体と炭酸水素ナトリウムの質量比が1.0:2.0なので、
1.6:x=1.0:2.0
という比例式が作れる。これを解くとx=3.2となるので、残った炭酸水素ナトリウムは
6.0-3.2=2.8
となり、2.8gが解答となる。
大問8 生殖
対立形質の純系どうしをかけ合わせて子を作り、自家受粉させて孫を作るというメンデルの実験結果からの出題だった。そのため、教科書の内容を押さえておけば問題なく解答できる単元であったといえる。
大問9 地球から見える金星
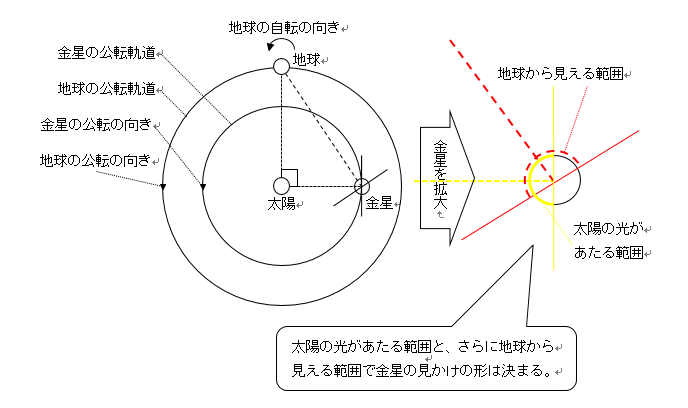
(3)では月の満ち欠けと異なり、地球-太陽-金星の順に作られる角度が90°になっても、地球から見える金星は半円ではない。その理由を正しく理解する必要があった。なお、半円に見えるのは、地球-金星-太陽の順に作られる角度が90°のときである。また、(4)では地球が1か月に360°÷12か月=30°公転し、金星は公転周期が約0.62年(=7.44か月)なので、1か月で360°÷7.44か月≒48°公転する。したがって、1か月で48°-30°=18°ずつ金星が地球に近づくという計算をする必要があった。
(3)地球から見える金星の形が半円より大きい理由
全体を通して
教科書内の本文および実験をしっかり確認しておくことで解答できる問題が多かった。また、「比例の関係は比例式で解く」は今年度の計算問題でも有効な手段となりえた。以下に挙げる比例の関係の問題を使い、普段から比例式の立式および計算の練習を積んでおくと良いだろう。
理科における比例の関係の一例
- ばねに加わる力とばねののび(フックの法則)
- 初期微動継続時間と震源からの距離
- P波、S波の到達する時間と震源からの距離
- 銅と酸素の化合する質量比(4:1)
- 電圧と電流(オームの法則)
- 一定時間における、電力と電力量