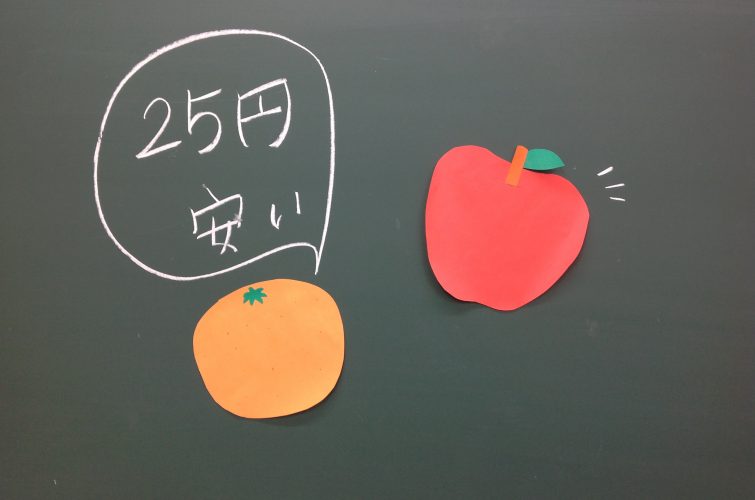
第5回 中受算数御用達!〇〇式のハナシ
みなさんこんにちは。早いものでもう12月、まだ済ませていないことは今年のうちに…と思いつつも特にコレというものは思いつかない井口です。
大体そういう事って忙しい時か締切ギリギリに思い出すんですよね。この仕組みどうにかならないものか…と毎年考えている気がします。
さて、前回、前々回とちょっと大きな話をしてしまったので、今回は我がフィールド、算数の世界に皆様をお連れします。中学受験の算数と聞くと、「難しい」というイメージと直結しやすいと思います。実際に勉強している子どもたち、またはかつてしていた現私立中生なら、どれだけ中学受験の算数が大変か、をよく御存じのはず。授業でどんなことを学習しているのかを、今回は少しですがお話ししたいと思います。最近4年生で「消去算」と呼ばれるものを学習しました。漢字だけ見ると「消し去る」、そうか問題ごと消し去りたいそんな問題…なわけはなくて、「二つのものから一つのものを消して、もう一方のものを求める」という考え方に基づく計算方法です。具体的に例題を上げて考えてみましょう(お、算数の先生っぽくなってきた!)。
【問】みかん2個とりんご3個で250円、みかん1個の値段はりんご1個の値段より25円安いです。みかん1個は何円でしょう。
大人なら、「アレで解けるんじゃない?」と解法についてピンときた方もいらっしゃるのではないでしょうか。そう、中学校で学習する「連立方程式」です。みかん1個をx円、りんご1個をy円とすると式が作れそうですね。いま、みかんをミ、りんごをリと表記して解いていくと、この文章題からは①「ミ×2+リ×3=250」と②「ミ×1=リ×1-25」という二つの式がたてられます。このあとは、②を2倍して、①とミの係数をそろえて「ミ×2=リ×2-50」という式にしてから、①の「ミ×2」の部分に「リ×2-50」を入れます。代入法ですね。このあと計算がつつがなくいけばみかん1個の値段は35円、となります。このように、中学以上の数学を知っていれば解けることを小学生でやる、それが中学受験の算数の根幹の一部をなすのです。
私自身、教えていて一番注意していることは一回学習しただけですぐに内容を理解することは大人が予想する以上に難しいものだ、ということです。授業を聞いただけで分かる内容はほとんどなく、宿題をする、授業ノートの見直しをする、テストの解き直しをする…こういうことを繰り返していくことで自分のものになっていく。逆に言えば、何度も目にして頭に入れていかなければ、なかなか一人でできるようにはならないということです。ですから、一回のテストで間違えたからといって「この前習ってきたでしょ!?」と反応してしまうことは、まだ学習途中のお子さんにとっては少し酷です。ですから、出来た問題にも目を向けてほしいのです。
「もうこんな問題も解けるようになったんだね!」という一言が、学校よりも先行く内容に日々取り組んでいるお子さんの気持ちをいかに力強く励ますことか。もちろん復習不足、準備不足での間違いには注意しなければなりませんが、同時にほめるということもどうぞよろしくお願いします。この積み重ねで受験を迎えるわけですが、小学6年生の今頃になると数年前では考えられないくらいにたくさんのことを自分のものにしていることになります。
未知との出会いが頻繁にあるのが中学受験の勉強ともいえるのですが、習ったことを自分のものにしていく過程を、自分で考えられるようになったらしめたもの!内容の習得について考えることも大切な勉強であり、財産です。難しいと思ったものでも、どうしたら自分の身に着くか考え、実行する。これが早い段階で出来るようになっていたら、お子さんにとって大きな味方になりますし、来る2020年の大学入試改革による影響の受け方が大きく、大きく異なると思います。勉強量ばかりがクローズアップされがちな中学受験ですが、勉強に向かう過程で精神的に得るものについても、魅力があると私は思います。そうそう、前々回にチラと登場させた「いもづる算」、これの例題を挙げますね。
【問】1個35円のみかんと1本40円のバナナを数本ずつ買ったところ、305円でした。みかんは何個買いましたか。ただし買った個数はみかんの方がバナナより少ないものとします。
井口からの挑戦状です!答えが出たら、または出ていなくても正解を知りたい場合、どうぞご連絡を!お待ちしております。